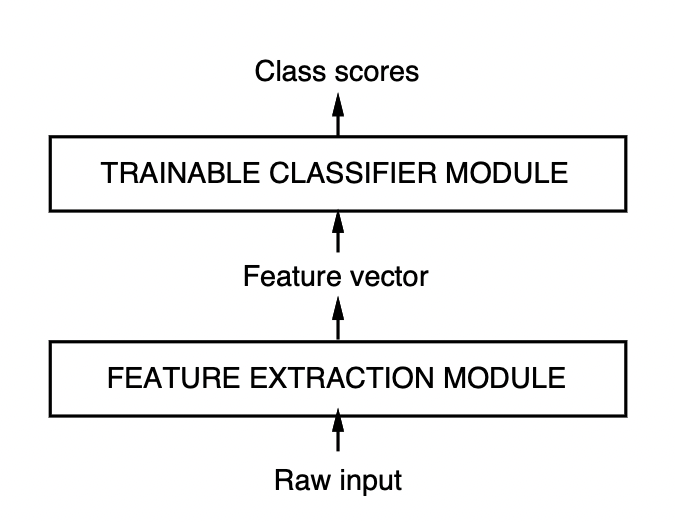
LeNet-5
LeNet-5
I. Introduction
learning techniques의 사용은 최근 성공적인 패턴인식 적용에 중요한 요인이다.
Feature Extractor( 특징 추출기 )는 사전지식이 많이 필요하고 진행중인 작업에 따라 다르다(ex> A와 B작업을 위한 특징 추출기는 다르다)
특징 추출기는 거의 전체를 대부분 사람이 직접 설계하기 때문에 설계에서 많은 집중이 필요하게 된다.
반면, Classifier( 분류기 )는 종종 범용적이고 학습 가능하다.
때문에 주요 문제점중 하나는 설계자의 적절한 특징 set을 적용하는 능력은 인식 정확도에 큰 영향을 주는 것이다.
각 새로운 문제를 해결하려 할 때 매번 다시 특징 추출기를 새로 설계해야 한다면 매우 힘들 것이다.
learning techniques 가 쉽게 분리되도록 저차원 공간으로 한정된 분류기에 의해 사용되기 때문에 적절한 특징 추출기의 필요했었다.
세 요인들이 뭉치면서 지난 위와 같은 수십년동안의 관점이 바뀌었다.
-
낮은 비용으로 수학적 계산이 빠른 컴퓨터를 사용
때문에 알고리즘적 개선보다 무차별적 수치대입 방법에 의존하게 되었다.
-
큰 시장과 폭넓은 관심이 있는 문제에 대한 대규모 데이터베이스의 가용성
때문에 인식 시스템 설계에서 직접 만든 특징 추출기보다 실제 데이터에 의존하게 되었다.
-
높은 차원의 입력 처리 능력과 큰 데이터를 통해 뒤얽힌 결정 함수를 만드는 능력을 가진 강력한 기계학습의 사용
때문에 음성과 필기 인식 시스템에 대한 정확도의 최근 진보는 학습 기술과 큰 학습 데이터에서 크게 기인되었다고 할 수 있다.
A. Larning from Data
자동 기계학습에 대하 접근중 가장 성공적인 접근은 ‘numerical’ 또는 gradient-based learning이라 불린다.
\[Y^p=F(Z^p,W)\\ E^p=\mathcal{D}(D^p,F(Z^p,W))\\ E_{train}(W)=Average(E^p)\]간단히 보면 학습은 $E_{train}(W)$을 낮추는 $W$를 찾는 것이지만
사실, 학습 데이터에서의 성능은 별로 중요하지 않다.
더 중요한 지표는 실제로 사용될 분야에서 그 시스템이 보이는 ‘오차율’이다.
이 ‘오차율’은 학습 데이터와 분리된 테스트 데이터에서의 정확도를 계산하여 평가한다.
테스트 데이터 오차율과 학습 데이터 오차율의 차이는 보통 다음과 같이 정의된다.
\[E_{test}-E_{train}=k(h/P)^\alpha\]P가 학습 데이터 수, h는 ‘effective capacity’로 기계의 복잡도를 나타낸다.
따라서 학습 데이터 수가 많아지면 오차율 gap이 항상 줄고
그리고 h값을 높이면 $E_{train}$값이 줄지만 $E_{test}-E_{train}$값인 오차율의gap이 커진다.
대부분 학습 알고리즘들은 $E_{train}$와 $E_{test}-E_{train}$을 최소화 하려고 한다.
이러한 것을 공식적으로 Structural Risk Minimization(구조적 결함 최소화)라고 부르고
각 하위 집합이 이전 하위 집합의 상위 집합이 되도록 매개 변수 공간의 하위 집합을 만드는것 처럼 기계가 학습을 하도록 capacity를 높이는 시퀀스를 기반으로 정의한다.
실제로 구조적 결함 최소화는
\[E_{train}+\beta H(W)\]를 최소화 시키도록 구현한다.
$H(W)$는 Regularization function(정규화 함수)이라 하고
$\beta$는 상수다
정규화 함수는 매개변수 공간의 하위집합중 high-capacity인 매개변수들 W에서 큰 값을 취하도록 선택된다.
H(W)의 최소화는 capacity가 접근 가능한 매개변수공간의 하위집합을 제한 한다.
그렇게 함으로써 학습 오차율과 두 오차율간의 차이의 tradeoff를 조절한다.
B. Gradient-Based Learning
매개변수 집합을 사용하는 함수의 값을 최소화 하는 문제는 컴퓨터 과학의 많은 문제의 근원이다.
손실함숫값은 매개변수의 작은 변화가 손실함수에 끼치는 영향을 측정하여 최소화 한다.( 손실함수를 매개변수에 대해 미분한 기울기를 통해 손실함숫값을 측정 )
해석적 미분이 가능할 때 효율적인 학습 알고리즘을 고안할 수 있다.( 반대는 perturbation을 통해 수치적으로 한다 )
최소화하는 가장 간단한 방법은 Gradient Descent 알고리즘이다.
\[W_k=W_{k-1}-\epsilon\dfrac{\partial E(W)}{\partial W}\]유명한 최소화 과정은 SGD(stochastic gradient descent, also called on-line update)이다.
\[W_k=W_{k-1}-\epsilon\dfrac{\partial E^{p_k}(W)}{\partial W}\]SGD는 기울기 평균의 근사치를 통해 매개변수를 업데이트한다.
가장 흔한 경우로 매개변수는 단일 샘플을 기반으로 업데이트 된다.
때문에 W는 평균 궤도에서 변동되지만 대개는 빅데이터에서 일반적인 경사하강법과 second-order방법보다 상당히 빠르게 수렴한다.
C. Gradient Back-Propagation
경사 하강 학습은 1950년대 부터 사용 됐지만,
대부분 선형 시스템으로 제한되었다.
복잡한 기계학습 작업에 대한 경사하강법의 놀라운 유용성은 아래 세가지 사건이 발생할 때까지 널리 실현되지 않았었다.
- 극솟값에 대한 존재가 실제로는 큰 문제가 되지 않는 다는 것을 깨달음
- 사실 극솟값이 다층 신경망에서 문제가 되지 않는다는 것이 이론적으로 미스테리하다.
- It is conjectured that if the network is oversized for the task ( as is usually the case in practice ), the presence of “extra dimensions” in parameter space reduces the risk of unattainable regions.
- 추측해보자면 네트워크는 실제 문제에서 필요한 경우보다 oversize되어있다면(대개 실제문제에서 그러함), 매개변수 공간에서 “extra dimensions”의 존재는 global minima에 도달하지 못하더라도 oversize된 parameter space에서 도달한 local minima가 tight한 parameter space에서 도달 해야하는 global minima일 확률이 올라가기 때문
- 비선형 시스템에서 간단하고 효율적으로 gradient를 구하기 위해 Back-Propagation이 대중화 되었다.
- sigmoid를 통해 다층신경망에 적용된 backpropagation이 복잡한 학습 문제를 해결한것이 증명되었기 때문이다.
제어이론에서 Lagrange formalism이 back-propagation을 유도하는 최고의 방법이고 다시 나타나거나 새로 등장하는 네트워크를 유도할 때에도 좋다.
D. Learning in Real Handwriting Recognition Systems
최고의 neural network인 Convolution Network는 연관있는 feature를 이미지 픽셀로부터 바로 추출 하도록 학습하게 디자인 되었다.
필기체 인식 문제중 가장 어려운 문제중 하나는 문자 하나하나를 인식하는것 뿐만 아니라, 단어나 문장으로부터 이웃한 문자들을 서루 분리하는 것도 어렵다. ( a process known as “segmentation”)
모델에서 시스템의 정확도는 “heuristic에 의해 segmentation된 quality”와 인식기의 문자나 여러 문자로 잘 분할되거나 잘 분할되지 못한 문자들을 “구별해내는 능력”에 달려있다.
잘못 분해된 문자들을 라벨된 데이터로 만들어야 하는 어려움 때문에 인식기가 잘 작동하도록 학습시키는 것은 큰 도전이 된다.
E. Globally Trainable Systems
대부분의 실제 패턴인식 시스템들은 multiple modules로 구성되어 있다.
ex> 문서인식 시스템은
- field locator( extract ROI )
- field segmentor
- recognizer
- contextual post-processor
로 구성된다.
각 모듈을 수동적으로 최적화하고 또는 학습시킨다.
각 모듈들을 조립하여 시스템을 완성시킨 다음
각 모듈별로 성능을 최대로 올리기 위해 파라미터를 조정하는데 이것은 별로 좋지 않다.
더 좋은 방안은 global error를 최소화 하기 위해 전체 시스템을 한번에 학습시키는 것이다.
만약 성능을 측정하는 손실함수 E가 tunable한 파라미터W에 대해 미분가능하게 만들어진다면, Gradient-Based Learningdmf 통해 극솟값을 구할 수 있다.
global loss function이 미분 가능하게 하기 위해
전체적인 시스템을 미분 가능한 모듈들로 feed-forward 네트워크로 설계한다.
\[\begin{align*} Z^p&=X_0\\ X_n&=F(W_n,X_{n-1})\\ \dfrac{\partial E^p}{\partial W_n}&=\dfrac{\partial F}{\partial W}(W_n,X_{n-1})\dfrac{\partial E^p}{\partial X_n}\\ \dfrac{\partial E^p}{\partial X_{n-1}}&=\dfrac{\partial F}{\partial X}(W_n,X_{n-1})\dfrac{\partial E^p}{\partial X_n} \end{align*}\]II. Convolutional Neural Networks for Isolated Character Recognition
복잡하고 다차원이고 비선형인 큰 데이터들을 경사 하강법으로 학습한 다층 네트워크의 능력은 이미지 인식 작업에 명백한 후보자가 된다.
CNN의 흥미로운 점은 특징 추출기가 스스로 학습한다는 것이다.
문자인식에서 전결합의 feed-forward 네트워크가 성공적으로 이루어지기위해 몇가지 문제점들을 해결해야 한다.
1. 일반적인 이미지는 수백가지의 픽셀들로 이루어져 있다.
100개의 hidden unit을 가진 전결합층은 수만가지의 가중치를 갖게 된다.
매개변수의 증가는 모델의 capacity를 높이고 많은 양의 학습 데이터를 필요로 한다.
게다가 많은 가중치를 저장하기 위해 메모리 수요가 증가해 하드웨어의 능력을 뛰어넘을 수 있다. translate나 loacl distortion 같은 변형을 FC Layer가 충분한 크기의 unit들로 해결할 수 있지만,
비슷한 패턴의 매개변수들이 여러 뉴런에서 확인될 것이다.
또한, 충분한 크기의 unit들을 제대로 학습 시키려면 많은 데이터도 필요하다.
하지만, CNN에서는 매개벼수 공간에서 가중치 구성의 복제를 억제함으로써 shift 불변성이 자동적으로 적용된다.
2. 전결합 구조의 결핍은 입력의 topology를 완전히 무시한다.
입력 변수는 학습에서 결과에 영향을 주지 않고 많은 순서로 입력될 수 있다.
하지만, 이미지나 time-frequency같은 음성 파일은 근처에 있으면 높은 correlation을 보인다.
Local Correlation은 local feature 추출하기에 좋다고 잘 알려져있다.
가까운 변수들은 edge나 corner같은 작은 범주에 구성원이 되기 때문이다.
CNN은 은닉 뉴런들의 receptive field를 지역적이 되도록 제한함으로써 local feature들을 추출한다.
A. Convolutional Networks
- Convolutional Netwrok는 shift, scale, distortion에 불변을 보장하기 위해 세가지 구조를 조합한다
- local receptive fields, shared weights( weight replication ), and spatial or temporal sub-sampling
각 층의 유닛들은 이전 층의 이웃된 작은 영역의 유닛들의 집합을 입력으로 받는다.
Local receptive fields에서 뉴런들은 기초적인 visual feature들을 추출한다.(ex> edge, end-point, corner,…)
distortion이나 shift는 다양한 눈에 띄는 feature들을 발생시킨다.
그리고 이미지의 한 부분에 유용한 elementary feature detector들은 전체 이미지에 유용할 가능성이 있다.
이런 내용을 접목시키기 위해 이미지에서 다른 위치에 있는 receptive field들을 가진 유닛들의 집합이 고유의 가중치 벡터를 갖도록 한다.
한 층의 유닛들은 평면을 구성하고 그 안에 유닛들은 같은 가중치 집합을 공유한다.
이러한 유닛들로 만든 평면을 feature map이라 한다.
feature map의 모든 유닛들은 이미지에서 각각 다른 부분에 같은 연산을 하게 된다.
완성된 convolutional layer는 몇개의 feature map으로 구성되고 여러개의 feature map은 각 위치에서 여러개의 특징을 추출한다.
LeNet-5의 첫번째 층은 6개의 feature map을 가지고 각 feature map은 5x5형태로 25개의 입력값(receptive field)을 받는다.
따라서 25개의 입력을 받는 각 유닛은 25개의 학습가능한 계수와 하나의 편향을 갖는다.
convolutional layer의 흥미로운 점은 입력 이미지가 shift되면, feature map out도 같은 양 만큼 shift된다는 것이다.
이러한 convolutional network의 특성이 shift와 distortion에 robust하게되는 이유이다.
일단 특징이 감지되면, 그것의 정확한 위치는 덜 중요해진다.
그 특징과 연관된 다른 특징의 대략적인 위치가 더 중요하다.
각 특징들의 정확한 위치가 패턴을 구분짓는 것과는 연관이 없을 뿐 아니라,
다른 문자 예시에서 다양한 위치를 갖기 때문에 오히려 해롭다.
특징의 정확한 위치정보를 제거하기 위해 sub-sampling layer를 사용한다.
sub-sampling layer를 사용하면 shift와 distortion에 대한 민감성도 줄어든다.
LeNet-5의 두번째 층은 sub-sampling layer이다.
2x2의 receptive field에서 평균을 취하고 편향을 더한다.
결과적으로 크기가 이전 층보다 반으로 줄어든다.
sub-sampling에서 가중치 파라미터가 작으면, 준선형 모드의 작동을 하고
단지 입력을 blur처리할 뿐이다.
sub-sampling에서 가중치 파라미터가 크면, 편향에 따라 “noisy OR” 또는 “noisy AND” 함수 기능을 수행한다.
convolution과 sub-sampling을 연달아 두면 “bi-pyramid” 결과를 만든다.
feature map은 늘어나고 spatial resolution은 줄어든다.
weight sharing 기술의 흥미로운 부가 효과는 자유 매개변수를 줄인다는 점이다.
자유매개변수가 줄면 기계의 capacity도 줄고 test error와 training error의 차이도 줄어든다.
B. LeNet-5
LeNet은 입력층 빼고 가중치 있는 7층의 구조로 되어있다.
입력은 32x32 pixel 이미지이다.(데이터베이스에서 가장 큰 문자의 크기보다 충분히 큰 사이즈이다.)
highest-level feature detector에서 보는 receptive field의 중앙에 stroke end-point나 corner같은 잠재적 특징이 될만한 것들이 나타나기 때문이다.
마지막 convolutional layer(C3)의 receptive field들의 중앙은 32x32인 입력의 중앙에 20x20인 영역을 만든다.
입력값은 normalized를 통해 -0.1~1.175로 변형해서 거의 평균이 0, 분산이 1로 만들어 학습을 가속화 했다.
C1
32x32 → feature maps 6@28x28
5x5 크기의 필터 6개를 통해 연산을 하고 input이 32x32이므로
padding=0, stride=1에 대한 결과로
feature maps 6@28x28이 나온다.
가중치 수 : $(필터크기+편향)\times특징맵수 = 156$
연결 수 : $(필터크기+편향)\times convolution연산수\times 특징맵수=122304$
S2
feature maps 6@28x28 → feature maps 6@14x14
14x14크기인 6개의 feature map으로 출력된다.
2x2의 입력을 받고 4개의 값을 더하고 학습가능한 계수를 곱하고 편향을 더한다.
그 결과는 sigmoidal 함수로 전해진다.
각 receptive field는 겹치는 부분이 없기 때문에 C1의 출력을 입력으로 받은 S2의 출력은 C1의 출력의 반절이 된다.
가중치 수 : 12 = (1+1)*6
연결 수 : 5880 = (3+1+1)1414*6
C3
feature maps 6@14x14 → feature maps 16@10x10
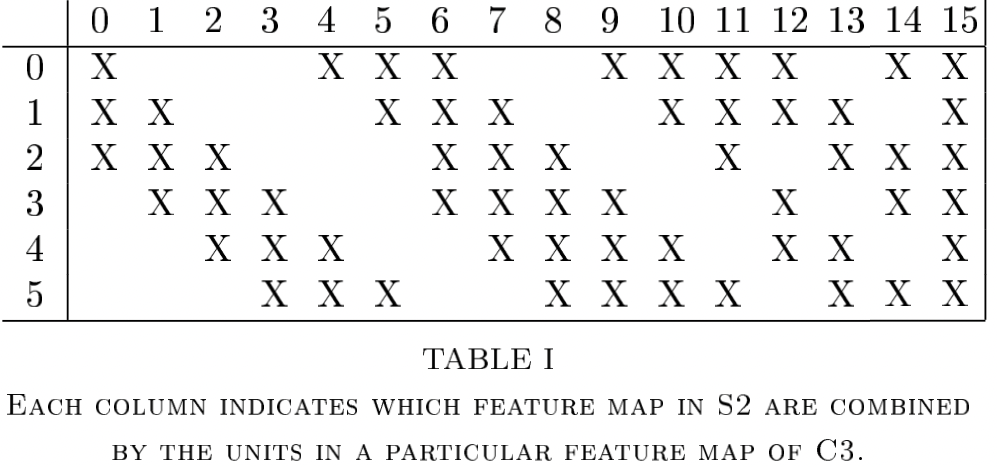
S2와 C3의 연결을 보면 S2의 모든 feature map이 C3의 모든 feature map에 연결되지 않는다.
첫 번째 이유
- 완전한 연결을 하지 않으면 연결의 수를 합리적인 범위로 제한할 수 있다.
- 더 중요한 것은 균형을 깬다는 것이다. 균형이 깨지면 서로 다른 입력을 받게 될 것이고 다른 특징들의 조합으로 서로 다른 상향된 특징을 얻을 수 있기 때문이다.
가중치 수 : 1516
연결 수 : 151600
S4
feature maps 16@10x10 → feature maps 16@5x5
가중치 수 : 32 = (1+1)*16
연결 수 : 2000 = (3+1+1)2516
C5
feature maps 16@5x5 → feature maps 120@1x1
필터의 크기가 그대로 5x5이고 feature map은 120개 이다.
따라서 출력의 모양이 120개의 feature map이고 그 크기가 1x1이 된다.
C5는 C3와 다르게 이전 층(S4)과 완전 연결을 한다.
이런 결과를 얻게 되는데도 C5가 Fully Connected Layer가 아니라 convolutional layer인 이유는 입력의 크기가 더 커지게 되면 C5의 결과는 1x1보다 커지기 때문이다.
가중치 수 : 48120 = (2516+1)120
연결 수 : 48120 = (2516+1)120
F6
120(feature maps 120@1x1) → 84
C5와 전결합을 이루는 84개의 유닛을 가진 층
가중치 수 : 10164 = (120+1)*84
연결 수 : 10164 = (120+1)*84
전통적인 신경망처럼, F6층까지는 입력벡터와 가중치벡터의 dot연산을 하고 bias를 더했다.
그리고 그 결과를 sigmoid squashing function에 입력했다.
\[x_i=f(a_i)\\ f(a)=A\ tanh(Sa)\]sigmoid squashing function으로 scaled hyperbolic tangent함수를 사용했다.
A는 함수의 amplitude이고 S는 원점에서의 경사를 결정한다.
따라서 함수 f는 +A와 -A에 수평 점근선이 있는 기함수이다.
A는 1.7159로 했다.
output
출력층은 Euclidean Radial Basis Function (RBF)으로 구성된다.
\[y_i=\sum_j(x_j-w_{ij})^2\]입력 패턴과 RBF와 연관된 class의 적합도를 측정한다.
값이 작을수록 관련있는 class
RBF는 분류할 클래스 수가 많아지더라도 잘 작동한다.
sigmoid와 달리 RBF는 원하는 특징이 아닌 영역을 보더라도 계산을 수행하기 때문에 목적이 아닌 class를 거부하는 용도로도 쓸 수 있다.
가중치의 범위를 1과 -1로만 구성하게 되면 sigmoid가 치솟는것을 막는데 그렇게 되면 손실함수가 천천히 수렴하는것을 방지한다.
C. Loss Function
LeNet-5에는 Maximum Likelihood Estimation criterion(MLE)가 사용될 수 있고 위에서는 Minimum Mean Squared Error( MSE )를 사용했다.
\[E(W)=\dfrac{1}{P}\sum^P_{p=1}y_{D^p}(Z^p,W)\]$y_{D^p}$ 는 $D_p$번째 RBF 결과이다.
이 손실 함수는 대부분의 경우에 적절하지만, 중요한 3가지가 빠져있다.
- RBF 매개변수를 adaptive하게 한다면, E(W)는 trivial solution을 갖는다 (Collapsing Effect) 하지만 이 문제는 RBF를 adaptive하게 안하면 일어나지 않게 해결할 수 있다.
-
competition이 없는 것이 두번째 문제이다. 더 차별적인 학습 기준에서 경쟁이 있을 수 있는데,ex> MAP(maximum a posteriori) criterion, 경쟁은 입력 이미지가 분류된 클래스이거나 어디에도 분류가 안되는 클래스일 수가 있다는 점에서 올바른 클래스일 확률을 최대화하는 것과 같다. penalty의 관점에서 보면, MSE는 올바른 클래스의 penalty를 작게 했다면 아래는 잘못된 클래스의 penalty를 끌어 올린다.
\[E(W)=\dfrac{1}{P}\sum^P_{p=1}(y_{D^p}(Z^p,W)+\log(e^{-j}+\sum_ie^{-y_i(Z^p,W)}))\]log항의 -값이 “competitive” 역할을 한다.
그 값은 손실 함수가 양수이기 위해 반드시 첫번째 항보다 작거가 같아야한다.
상수 j는 양수이고 class의 penalty가 이미 큰것을 더 커지지 않게 막는다.
쓰레기 클래쓰의 posterior probability는 $e^{-j}$와 $e^{-j}+\sum\limits_ie^{-y_i(Z^p,W)}$의 비율이 될것이다.
이 차별적인 기준은 RBF의 중심을 서로 떨어져 유지 시킴으로써 “collapsing effect”를 막는다.
III. Results and Comparison with other methods
개별 숫자를 인식하는 것은 실용적인 인식 시스템에 속한 많은 문제들중 하나지만, 모양을 비교하는 인식 방법의 성능을 아는데에는 훌륭한 기준이다.
많은 방법들이 직접 만든 특징 추출기와 학습 가능한 분류기의 조합으로 구성되지만, 이 논문은 normalized된 크기의 이미지에 바로 사용할 수 있는 적용가능한 방법에 집중한다.
A. Database: the Modified NIST set
NIST’s Special Database 3와 Special Database 1을 사용한다.
SD3는 학습데이터이고 SD1은 시험데이터이고 SD3가 SD1보다 clean 한다.
SD3는 Census Bureau(미국 인구조사국)에서 얻은 것이고 SD1은 고등학교 학생들로 부터 얻었기 때문이다.
학습 경험으로부터 현명한 결론을 도출하려면 전체 샘플에서 학습과 시험 데이터중 어느 것을 선택했는지와 무관하게 결과가 나와야 한다. ( 따라서 둘을 섞는다 )
SD1에서 첫 250명의 데이터는 학습데이터로 SD1에서 나머지 250명의 데이터는 테스트데이터로 각 데이터가 약 30000개가 되었고 SD3를 통해 각 데이터를 60000개로 만들어 줬다.
실험에는 10000개의 테스트데이터만 사용한다.(SD1과 SD3로부터 5000개씩) 그리고 학습데이터는 60000개 모두 사용한다.
세가지의 데이터베이스가 사용되었다.
- regular database 28x28 사이즈이고 가운데에 위치하게 함 어떤 경우에는 배경과 함께 32x32인 것도 있다.
- deslanted database deslanting과 cropped down으로 20x20으로 함 deslanting은 pixel inertia의 second moment를 계산(counting a foreground as 1 and a background as 0) 그리고 line의 shear 변환을 통해 principal axis가 수직을 이루게 한다.
- 옛날에 썼던 데이터로 크기가 16x16이다.
B. Results
LeNet-5는 regular database를 사용 전체 학습데이터 학습을 20번 수행 학습률 → ~2 : 0.0005 → ~5 : 0.0002 → ~8 : 0.0001 → ~12 : 0.00005 → ~20 : 0.00001
각 iteration전에 diagonal Hessian 은 500개 샘플로 재평가하고 iteration 끝날때까지 유지
매개변수들 사이에서 효과적인 학습률은 0.00007~0.016 사이이다.
10 iter까지 test error는 0.95%이고
19 iter후에는 0.35%였다.
많은 저자들이 NN을 다른 adaptive 알고리즘을 다양한 작업에서 학습 시키는 경우 over-training 현상을 관찰했다.
over-training이 발생하면, training error는 계속 감소하고 test error는 작아지다가 커진다.
이런 현상이 일반적이지만, LeNet-5에서는 볼 수 없었다.
가능한 이유로는 학습률이 비교적 컸기 때문이라고 할 수 있다.
가중치가 local minima에 수렴하지 않고 무작위로 진동하는 것이 over-training의 현상이다.
이러한 진동 때문에 그 평균 비용은 broader minimum에서 더 낮아지기 때문이다.
그래서, Stochastic gradient는 regularization에서 broader minima를 선호하는 비슷한 현상을 보일것이다.
Broader minima는 generalization error가 높아지는 매개변수 분포의 entropy가 커지는 경우에 solution과 일치한다.
학습데이터의 수가 많아지면 정확도가 향상된다.
왜곡된 데이터를 학습한 네트워크는 20번의 iter동안 두번만 각 개별 샘플을 효과적으로 본다는 것이 흥미롭다.
비록 나타나지 않았던 형태로 쓰여졌지만 어떤 것은 정말 애매하더라도 어떤 것은 사람이 완벽하게 분류할 수 있다.
때문에 더 많은 학습 데이터를 통해 개선 가능하다고 기대된다.
C. Comparison with Other Classifiers
C.1 Linear Classifer, and Pairwise Linear Classifier
\[\mathsf{Linear<[deslant]Linear<Pairwise\ Linear}\]C.2 Baseline Nearest Neighbor Classifier
K-nearest neighbor 분류기는 입력 이미지 사이에 Euclidean 거리를 측정한다.
이것의 이점은 학습시간이 필요없고, 설계자의 뇌가 필요없다는 것이다.
하지만, 메모리 수요가 크고 인식하는데 시간이 오래 걸린다.
1pixel = 1 byte → 20x20 pixel = 400byte → 60000x(20x20) pixel = 24000000byte = 24Megabyte
24Megabyte가 run time에서 사용가능해야함
많은 표현이 들어가면 error rate가 조금 올라갈 수 있다.
원래 실제 유클리드 거리 NN시스템은 특징 벡터들 사이의 연산을 하지만, 이 논문에 모든 시스템들은 픽셀들 사이에 연산을 하기 때문에 이 결과는 baseline comparison에 유용하다.
C.3 Principal Component Analysis (PCA) and Polynomial Classifier
40개의 principal component를 사용
821개의 입력을 받는 선형 분류기로 보일수 있다.
C.4 Radial Basis Function Network
첫 층은 28x28의 입력을 받는 1000개 가우시안 RBF유닛이다.
두번째 층은 1000개의 입력을 받고 10개를 출력하는 선형 분류기이다.
RBF 유닛들은 100개씩 10개의 그룹으로 나뉘고 K-means알고리즘을 통해 각 그룹은 학습을 한다.
두번째 층에서 가중치들은 pseudo-inverse 방법으로 regularized를 통해 계산된다.
C.5 One-Hidden Layer Fully Connected Multilayer Neural Network
또다른 분류기는 하나의 전결합층이 은닉층 전부이고 하나의 출력층을 갖는 역전파 알고리즘을 이용한 다층 신경망이다.
regular test data를 사용하면 300개의 은닉뉴런을 사용할 때가 1000개의 은닉뉴런을 사용할 때보다 test error가 높았다.
distortion이 적용된 데이터로 학습하면 전체적으로 개선이 되고 300개의 은닉뉴런일 때가 1000개의 은닉뉴런일 때보다 test error가 작았다.
deslanted data를 학습하면 300개의 은닉뉴런일 때 test error가 1.6%까지 떨어졌다.
자유 매개변수가 많을 수록 test error가 낮게 나온다.
→ self-regularization을 한다고 추측한다. 가중치 공간에서 원점은 saddle point이기 때문에 어느 방향으로든 SGD가 보기에는 매력적으로 보이기 때문이다. 첫 몇번에 epoch에서만 가중치가 줄지 않음.
작은 가중치는 sigmoid를 준선형으로 작동하게 하여 network는 low-capacity가 되어 마치 sigle layer network처럼 된다.
C.6 Two-Hidden Layer Fully Connected Multilayer Neural Network
이론상 어떤 기능도 하나의 은닉층 신경망으로 근사화될 수 있다.
그러나, 두 은닉층 신경망이 가끔 실제 상황에서 더 좋은 성능을 보였다.
여기서도 그 현상을 관찰했는데, 28x28-300-100-10 network에서 test error가 3.05%로 은닉층이 하나인 경우보다 뛰어났다.
network 크기를 28x28-1000-150-10으로 늘린 경우에는 조금 개선된 test error가 2.95% 였다. 28x28-300-100-10가 training with distorted pattern으로 된 경우 약간 개선된 2.50%다.
그리고 크기를 키워서 28x28-1000-150-10일 때는 2.45%였다.
C.7 A Small Convolutional Network: LeNet-1
Convolutional network는 딜레마를 풀려고 한다.
작은 network는 학습을 할 수 없고 큰 network는 매개변수가 너무 많은 딜레마
이미지는 16x16으로 줄이고 28x28크기의 가운데에 위치 시켰다.
100000번의 계산이 필요하지만 convolution의 특징으로 자유 매개변수는 2600개 뿐이다.
LeNet-1은 USPS 데이터 형식에 만들어졌고 입력을 위해 다시 조절했다.
test error는 1.7%가 나왔다.
적은 수의 매개변수로 error가 작게 나오는 신경망은 그 구조가 적용될 작업에 적합하다는 것이다.
C.8 LeNet-4
LeNet-1에서 convolutional network가 크면 큰 사이즈의 학습 데이터에 적합해진다고 보았다.
LeNet-4와 LeNet-5는 이 문제를 해결하기 위해 고안되었다.
LeNet-4는
Conv1(4)→Sub2(8)→Conv2(16)→Sub3(16)→FC4(120)→output
free parameters : 17000
connections : 260000
test error : 1.1%
실험에서 분류기는 유클리드 NN 분류기를 사용했다.
C.9 Boosted LeNet-4
여러개의 분류기를 조합해 “boosting” 방법을 만들었다.
3개의 LeNet-4를 조합했다
- 하나는 일반적 방법으로 학습시켰고
- 두 번째는 첫번째 네트워크의 분류 결과를 가지고 학습했다.
- 세 번째 네트워크는 앞에 네트워크들과 일치하지 않는 새로운 패턴에 대해 훈련했다.
test하는 도안, 세개의 네트워크의 결과를 단순히 더했다.
왜냐하면 LeNet-4의 error는 괸장히 작기 때문이다.
그리고 두 번째와 세 번째 네트워크를 학습 시키기 위해 인공적으로 왜곡시킨 학습 데이터를 사용했다.
test error : 0.7 %
boosing이 3배 더 비용이 들어 보이지만 사실, 첫 번재 네트워크가 정답에 높은 자신을 보이면 두 번째와 세 번째 네트워크는 호출되지 않는다.
따라서 계산 비용은 LeNet-4가 하나인 경우보다 boosting에 경우 1.75배만 증가했다.
C.10 Tangent Distance Classifier ( TDC )
TDC는 입력 이미지의 작은 왜곡과 이동에 민감한 거리측정 함수가 사용된 nearest-neighbor 방법이다.
만약 고차원 공간에서 이미지를 점 하나로 생각할 때, 문자의 왜곡은 픽셀 공간에서 곡선을 따라간다.
같이 취해진 이 모든 왜곡들은 픽셀 공간에서 낮은 차원의 다양성을 정의한다.
원본 이미지에 가까운 작은 왜곡들로인한 다양성은 tangent plane으로 추측될 수 있다.
여러 왜곡들을 사용해 만든 tangent plane들 과의 거리를 통해 “closeness”를 측정한다.
test error : 1.1% (입력 16x16)
유클리드 거리를 통해 여러 결과들을 사전에 필터링하면 tangent 거리 계산을 줄일 수 있다.
C.11 Support Vector Machine (SVM)
Polynomial 분류기들은 복잡한 결정 평면을 만들 때 잘 학습되는 방법이다.
하지만, 제공되는 항의 수가 제한적이라 고차원 문제를 풀기에는 실용적이지 못하다.
SVM은 고차원 공간에서 다항식이나 많은 평면을 포함하는 복잡한 평면을 나타내는 매우 경제적인 방법이다.
regular SVM test error : 1.4%
Cortes and Vapnik test error : 1.1%
계산 비용이 매우 높다.
V-SVM test error : 1.0%
modified V-SVM test error : 0.8%
하지만, V-SVM은 regular SVM의 2배 만큼 비용이 높다.
Burges는 Reduced Set Support Vector technique(RS-SVM)을 제안하고 1.1%의 test error를 얻었고
계산 비용은 LeNet-5보다 60%만큼만 높았다.
D. Discussion
Boosted LeNet-4의 성능이 제일 좋고 그 다음이 LeNet-5이다.
신경망은 memory 기반 방법들보다 계산 수가 적다.
일반적인 구조와 그들의 적은 메모리 수요 때문에 CNN들은 하드웨어 구현에 특히 적합하다.
LeNet-5이전 analog와 digital을 섞어서 구현한 네트워크는 초당 1000자를 넘는 속도로 계산해왔다.
그러나, 컴퓨터 주요 기술의 급진적 진보로 인해 섞어서 만든 네트워크들을 쓸모없게 만들었다.
메모리 기반 기술들은 메모리와 컴퓨팅에 대한 수요가 커서 비용 효과적 구현에서는 피한다.
KNN과 TDC는 학습 시간이 없다고 단층 네트워크, pairwise 네트워크, PCA+quadratic 네트워크 1시간 내로 학습하고 다층 네트워크는 더 오래 걸린다.
CPU로 LeNet-5를 학습시키는데에는 2~3일이 걸렸다.
학습 시간은 설계자가 고려할 사항이고 최종 시스템 사용자와는 별로 관계가 없다는 것을 알아야 한다.
현존하는 기술과 그것보다 학습시간이 늘고 조금 상향된 정확도의 새로운 기술중에 최종 사용자는 새로운 기술을 택할 것이다.
대부분의 방법들은 적절한 성능을 위해 1byte만 필요하지만 Nearest-Neighbor방법은 pixel당 4bits만 필요하다.
게다가, 신경망은 메모리 기반 방법보다 더 적은 메모리를 수요한다.
전반적인 성능은 많은 요인에 기인한다(정확도, 실행시간,메모리 수요).
컴퓨터 기술이 상향되면, larger-capacity recognizers도 가능해진다.
larger recognizer는 더 큰 학습 데이터를 필요로 한다.
LeNet-1은 1989에 사용하기 적절했고 LeNet-5는 1998에 사용하기 적절하다.
1989년도에는 LeNet-5 정도의 복잡한 인식기는 학습하는데 몇주가 걸리고 더 많은 데이터가 필요했기 때문에 사용하려고 생각하지도 않았다.
boosting이 메모리와 계산비용에 적당한 증가를 주지만 많은 개선력을 준다는걸 알았다.
도한, 왜곡을 통해 데이터의 양을 효과적으로 늘려서 실제로 많은 데이터를 모아야 될 필요가 없어졌다.
SVM은 훌륭한 정확도를 갖지만 사용에 대한 비용이 높아 Reduced된 형태로 사용했더니 CNN의 error rate와 비슷했다.
신경망은 메모리 기반 방법보다 더 빠르고 더 적은 공간을 필요로하기 때문에 데이터의 사이즈가 커질수록 더 뛰어난 성능을 보인다.
E. Invariance and Noise Resistance
convolutional network는 특히 다양한 사이즈, 위치, 방향, 사람에 의한 분할같은 형태를 거부하거나 인식하는데 적합하다.
글자 분할기는 완벽하지않아서 기울어지거나 중심에 있지 않거나 크기가 다르거나 할 수 있어서 분류기의 invariance는 중요하다.
완벽한 불변성을 가지는 분류기를 만드는 목표는 해결하기 어렵지만 CNN은 그 문제에 대한 어느정도 해답이 된다.